Warning
This version of the documentation is NOT an official release. You are reading the documentation version which is in active and ongoing development.
Noise current injection into single neurons¶
To account for additional effects seen in recordings from real nerve cells, we add some noise current to the input mimicking spontaneous channel openings, or synaptic bombardment originating from a large pool of presynaptic neurons. If the fluctuations of a physical variable are due to the combined influence of a large number of small contributions, the concept of White Noise can provide an adequate descriptive model. In this idealized type of signal, all frequencies are present in equal proportions, but with random phases (wind). A well-known example is white light, which comprises all colors from the visible spectrum. In our simulations, we use a sequence of independent identically distributed Gaussian random variables to approximate a particular type of white noise, Gaussian White Noise (GWN).
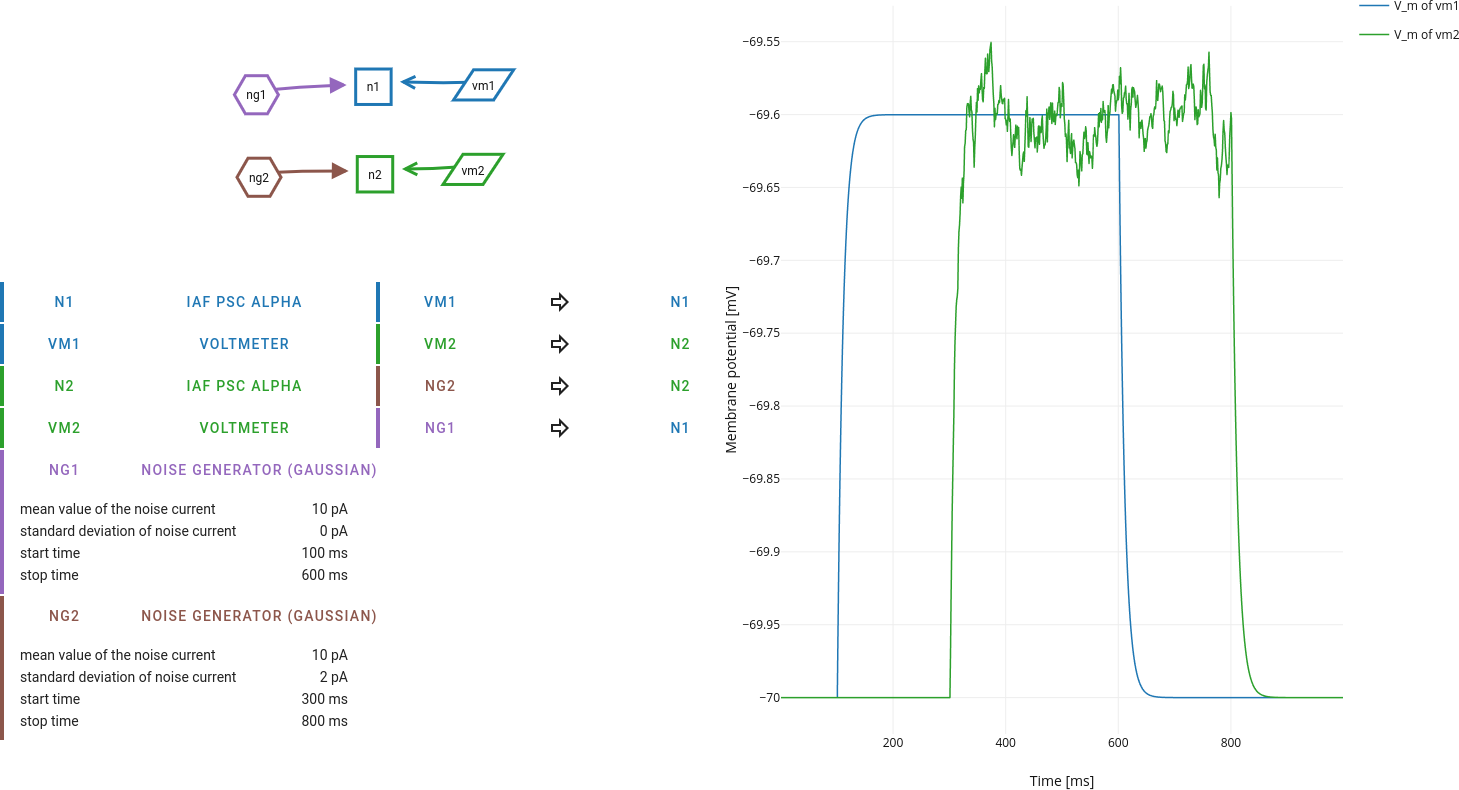
First look at the effect of noise in the subthreshold case. While you explore the membrane potential response for (weak) noise current input, note that GWN, like any Gaussian random variable, has two parameters: mean and variance.
Perform systematic simulations with different combinations of mean and variance (or standard deviation) and find a way to document the results.
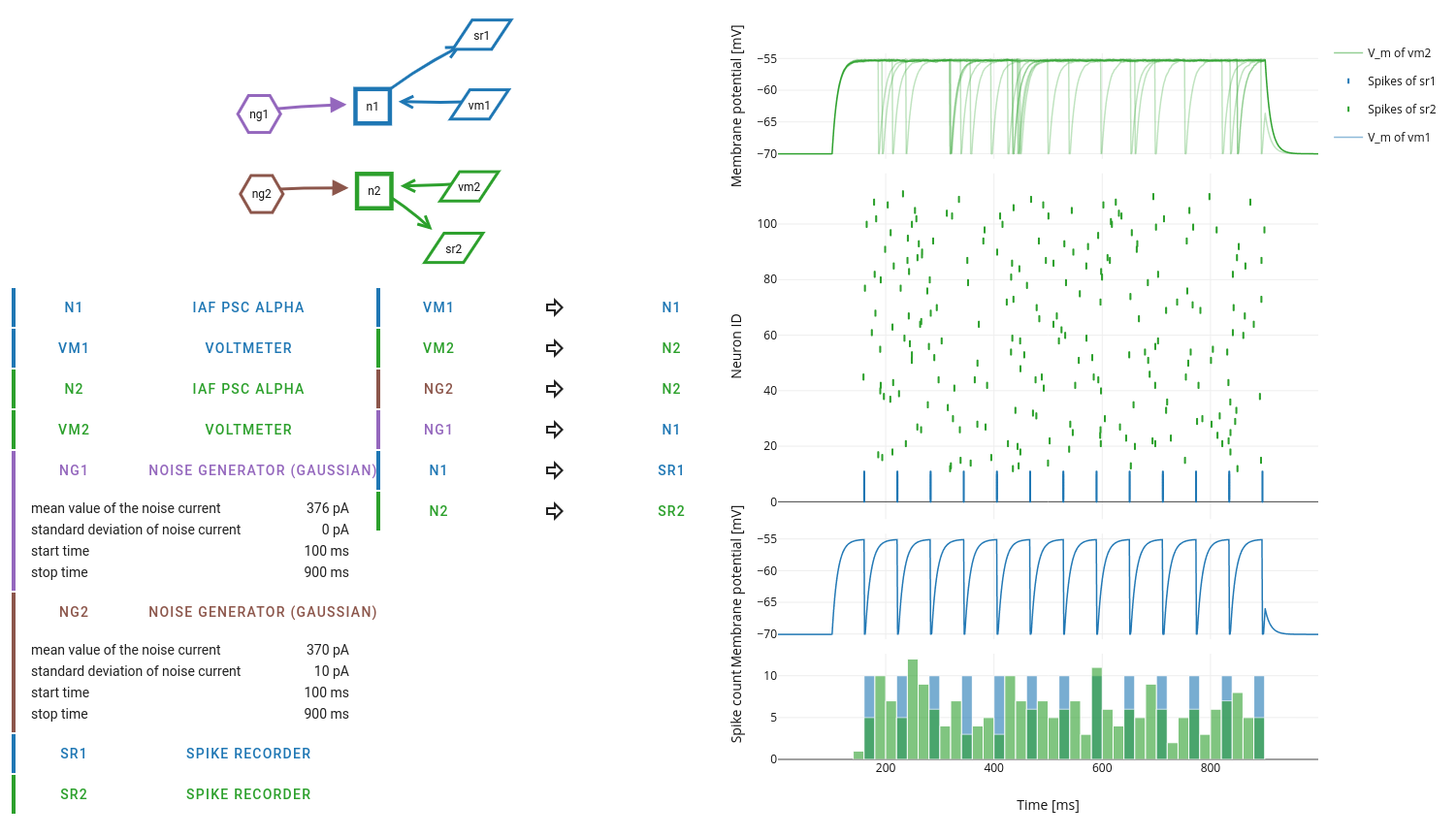
Now, consider a spiking neuron with “strong” noise current as input. If the strength of the input (mean), or the amplitude fluctuations of the input (variance), are large enough, the firing threshold is crossed and action potentials are generated. In contrast to the case of DC input, the fluctuations of the membrane potential will now affect the timing of the action potentials to some extent.
Document this phenomenon with a suitable set of experiments, where you run the simulations with different seeds of the random number generator.
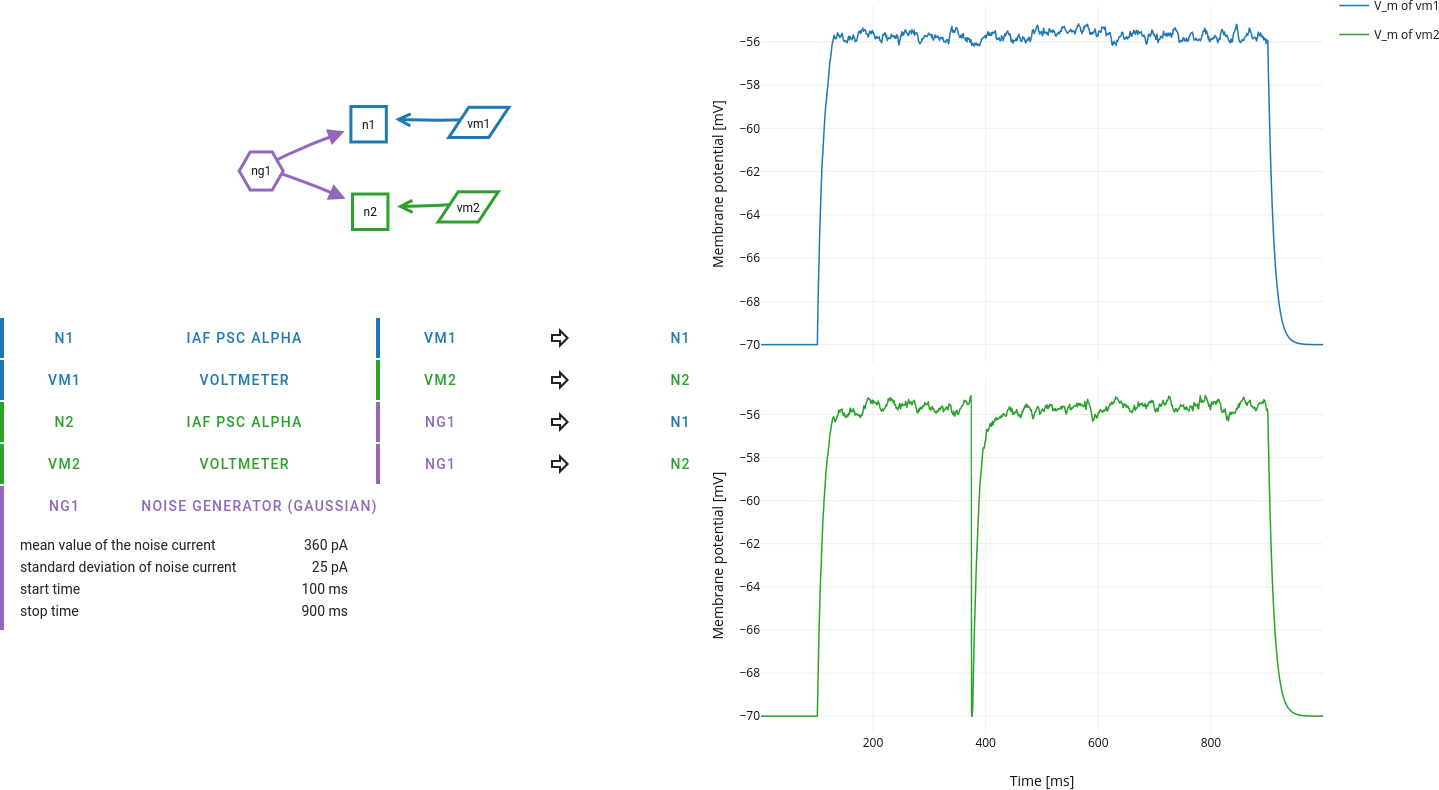
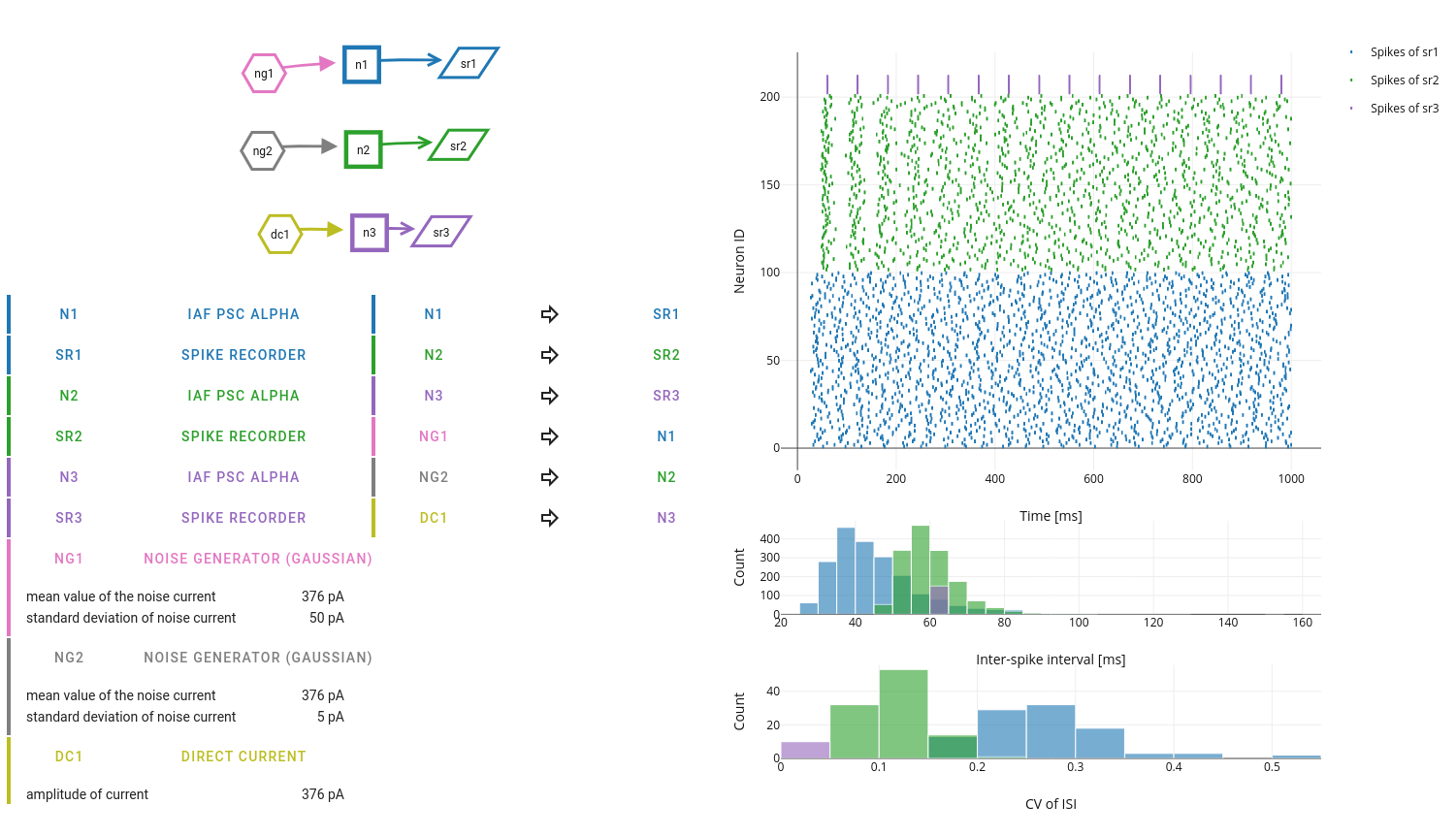
Play with the parameters of the noise current over a certain range of values when there is
no action potential generated, and
several spikes generated.
What exactly is the “threshold” now? To judge the effect of random fluctuations, it is important to look at multiple repetitions of the same experiment.
What happens to the frequency of spikes and the irregularity of spike trains as mean and/or variance of the noise is increased? The irregularity of neuronal spiking can be assessed, for example, by the coefficient of variation (CV) of the inter-spike intervals.
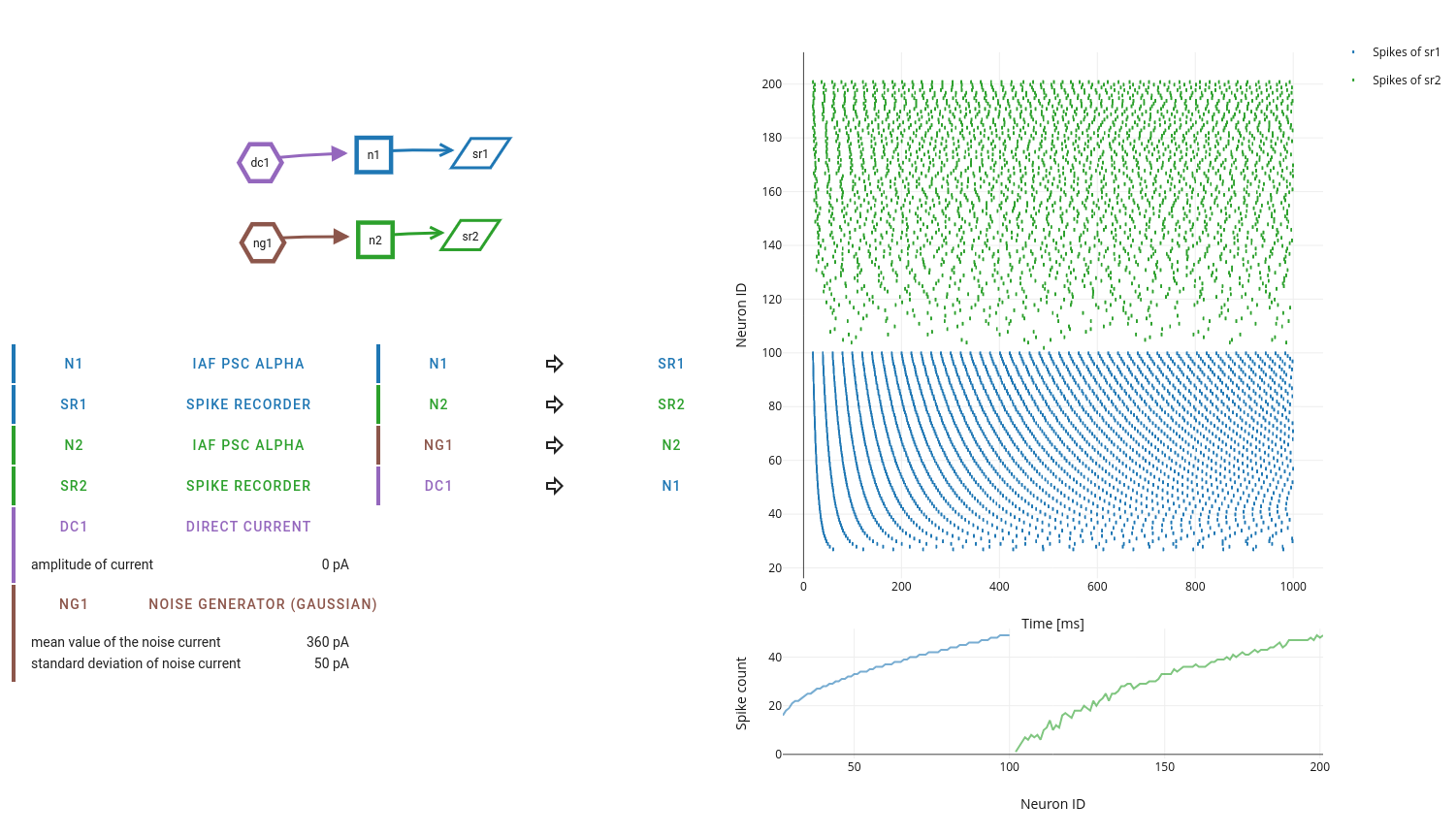
Now you should systematically measure two types of input-output curves of the neuron:
Keep the variance of the noise at a fixed level and systematically change the mean of the noise. What is the difference to the curve you obtained with pure DC input?
Now keep the mean of the noise at a fixed level and systematically change the variance of the noise. What is the minimal variance (“threshold”) that leads to a non-zero response rate?