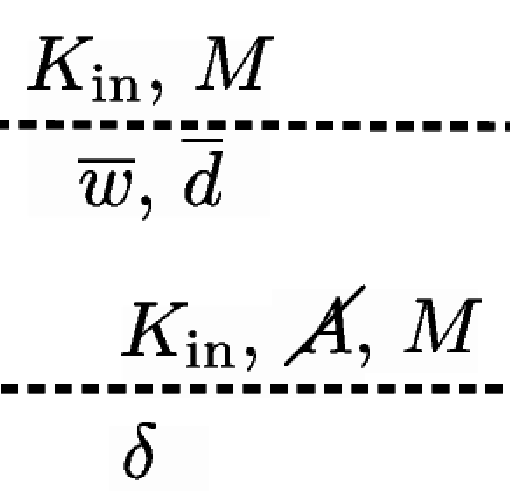Network graph¶
Graphical representations are a direct expression of how researchers think about a network model. They convey an intuitive understanding of network structures, relationships, and other properties central to the dynamics, and may also reflect how a model is implemented. If similar diagram styles are used, diagrams facilitate the reading of an article and allow for comparability of models across publications.
For visually constructing and inspecting network graphs, NEST Desktop builds on the graphical notation introduced in the article “Connectivity concepts in neuronal network modeling” [1]. We suggest to cite this article as a permanent reference for the proposed notation, while this documentation serves as a living reference allowing for further modification.
Here, we define the graphical elements used for Network nodes and Edges. We also provide details on the conventions for the Annotation of an edge as introduced in [1], even though they are presently not included in the NEST Desktop interface, and finally we show an Example.
Network node¶
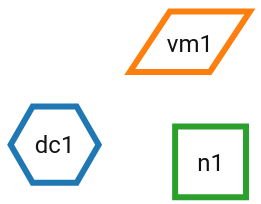
A network node in the notation represents one or multiple units. These units are either neuron or neural population models, or devices providing input or output. Network connectivity is defined between these graphically represented nodes. Nodes are drawn as basic shapes. A textual label can be placed inside the node for identification. Nodes are differentiated according to a node class and a node type.
Node class¶
The node class determines if a node represents an individual unit or a population of units by different frames of the shapes depicting the nodes. The distinction is a recommendation for diagrams that contain both kinds of nodes.
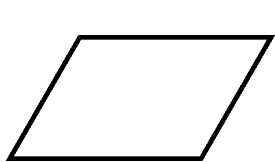
Individual unit

Population

Node type¶
The node type refers to a defining property of a node and is expressed by a unique shape.
Generic node

Excitatory neural node

Inhibitory neural node

Stimulating device node
Recording device node
Node label¶
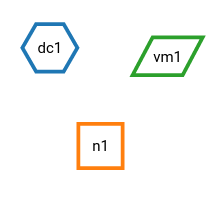
Each node graph is labeled to identify the model of the node. By default, it creates a direct current generator (dc) for a stimulus and a voltmeter (vm) for a recording device. Neurons are just labeled with (n). You can find the full label of the node model in the network controller.
Note: Node label is not defined in [1].
Node color¶
In NEST Desktop, nodes and connections contain parameter configurations which are displayed in the controller panel in the side navigation. The color of nodes helps you to associate the network graph with the controller as well as the corresponding visualization of the network activity.
Note: Node color is not defined in [1].
Network edge¶
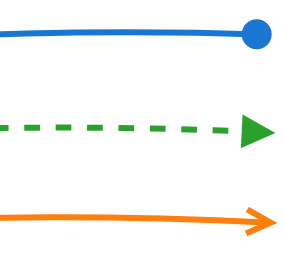
A network edge represents a connection or projection between two nodes. Edges are depicted as arrows. Both straight and curved lines are possible. Edges are differentiated according to the categories determinism, edge type, and directionality.
Determinism¶
The notation distinguishes between deterministic and probabilistic connections via the line style of network edges. Edges between two nodes representing individual units are usually deterministic.
Deterministic

Probabilistic

Edge type¶
Analogously to the node type, the edge type emphasizes a defining property of the connection by specific choices of arrowheads. The edge types given here can be used for connections between all node types.
Generic edge

Excitatory edge

Inhibitory edge

Directionality¶
Unidirectional

Bidirectional

Edge color¶
The edge color is determined by the color of the source node.
Note: Edge color is not defined in [1].
Annotation¶
Network edges can be annotated with information about the connection or projection they represent. Details on the rule specifying the existence of connections and their parameterization may be put along the arrow.
Note: Annotation is not available in NEST Desktop.
Connectivity concept¶
The properties in this category further specify the presence or absence of connections between units within the connected nodes.
Concept¶

The definitions and symbols given in the connectivity concepts defined in [1] (for a permanent reference) and in the Connectivity concept (for a living reference) are the basis for this property.
Constraint¶

Specific constraint or exception to the connectivity concept.
Parameterization¶

Properties of the parameterization of connections, e.g., of weights \(w\) and delays \(d\), can be expressed with mathematical notation.
Further specification¶

Annotations for both the connectivity concept and the parameterization of connections can be specified further.
For a discussion on customization and extension see [1].
Example¶
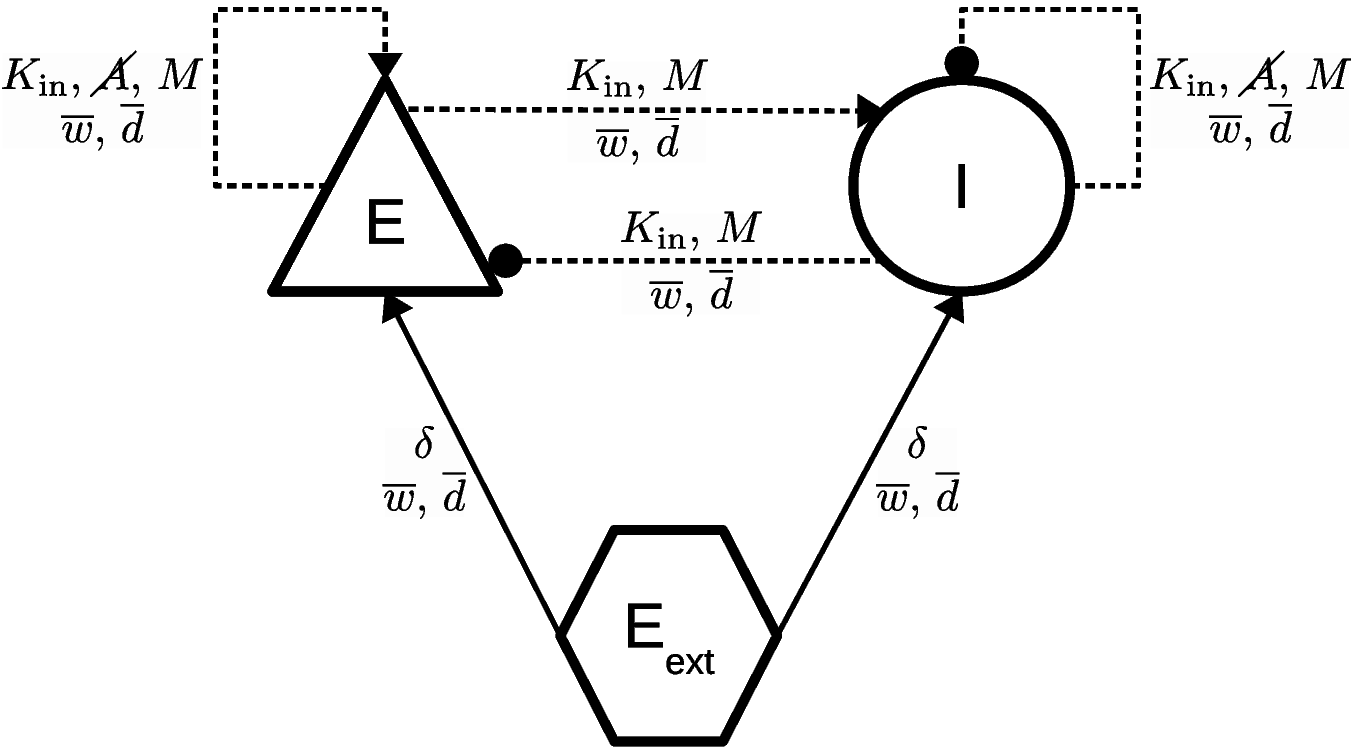
Graphical notation
NEST Desktop
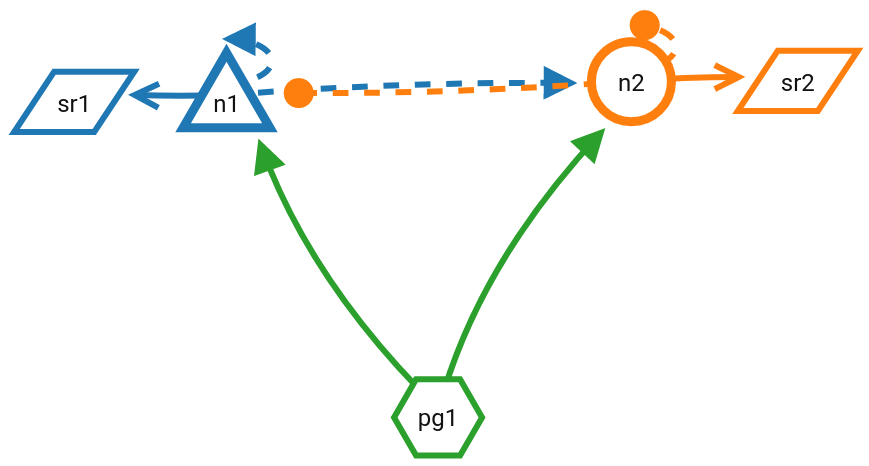
The example is a balanced random network model with the random, fixed in-degree connectivity. The illustration uses the elements for nodes, edges, and annotations introduced above to depict the network composed of an excitatory (E, triangle) and an inhibitory (I, circle) neuron population, and a population of external stimulating devices (\(E_\text{ext}\), hexagon). Recurrent connections between the neurons in the excitatory and inhibitory populations are probabilistic (dashed edges) and follow the “random, fixed in-degree” rule (\(K_{in}\)) with the further constraints that autapses are prohibited (\(\cancel{A}\)) and multapses are allowed (\(M\)).
Here, the NEST Desktop version also displays spike recorders.
Note: Annotations are not available in NEST Desktop.
To generate static publication-ready visualizations of network graphs in agreement with the graphical notation (corresponding to the figure on the left), please refer to this lightweight LibreOffice extension for the graphical notation.
Further examples can be found in [1].
References¶
| [1] | (1, 2, 3, 4, 5, 6, 7, 8) Senk J, Kriener B, Djurfeldt M, Voges N, Jiang HJ, et al. (2022) Connectivity concepts in neuronal network modeling. PLOS Computational Biology 18(9): e1010086. https://doi.org/10.1371/journal.pcbi.1010086 |